MKL1888:Pyromēter
[486] Pyromēter (griech., Hitzemesser), Apparate zur Messung hoher Temperaturen, sind nach den verschiedensten Prinzipien hergestellt worden; aber durch keins der bisher angegebenen Instrumente wird die schwierige Aufgabe in vollkommen befriedigender Weise gelöst. Das Luftthermometer (s. Thermometer) wird zum P., wenn man sein Gefäß aus einem Material verfertigt, welches hohe Temperaturen vertragen kann. Am besten eignet sich hierzu gut glasiertes Porzellan, während das von Pouillet bei seinem Luftpyrometer angewendete Platin bei hoher Temperatur Gase durchläßt. An einem Quecksilbermanometer, dessen einer Schenkel mit jenem Gefäß in Verbindung steht, während der andre offen bleibt, mißt man entweder, wie Pouillet, die Ausdehnung der eingeschlossenen Luft bei gleichbleibendem Druck, oder man bestimmt, wie Regnault, die Drucksteigerung bei unverändertem Volumen, woraus sich dann mit Hilfe des bekannten Ausdehnungskoeffizienten der Luft die Temperatur, welcher

| |
| Fig. 1. Petersens Gewichtspyrometer. | |
das Gefäß ausgesetzt wurde, leicht berechnen läßt. Ein sehr einfaches Luftpyrometer, welches man Gewichtspyrometer nennen könnte, wurde von Petersen angegeben. Dasselbe besteht aus einem Platinfläschchen (Fig. 1) von ungefähr 10 ccm Inhalt, dessen Mündung durch eine lose aufgesetzte Schraube weder luft- noch wasserdicht verschlossen wird. Der Apparat wird in einem Graphittiegel in den erhitzten Raum gebracht, alsdann in Wasser geworfen, wo er vermöge seiner Konstruktion von selbst die Mündung nach abwärts kehrt; durch Wägung des eingedrungenen Wassers erfährt man das Volumen der durch Ausdehnung entwichenen Luft, woraus sich leicht die Temperatur berechnen läßt, welcher der Apparat ausgesetzt war. Durch Erman und Herter wurde die Einrichtung dieses Pyrometers verbessert. Auf der Ausdehnung fester Körper beruht das Metallpyrometer von Daniell. In Graphitmasse eingebettet liegt ein Platinstab, welcher, indem er sich stärker ausdehnt als jene, eine Porzellanstange verschiebt und dann liegen läßt. Durch eine Art Fühlhebel wird diese Verschiebung nach dem Erkalten gemessen und aus der bekannten Ausdehnung des Platins die Temperatur berechnet. Das auf demselben
| |
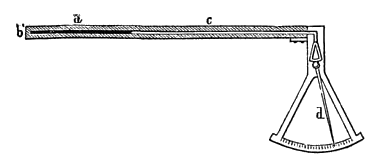
| Fig. 2. Petersens Metallpyrometer. | |
Prinzip beruhende P. von Petersen (Fig. 2) besteht aus einem Platinstab a, der am Ende b einer Eisenröhre befestigt ist und sich mit seinem andern Ende in einen Eisenstab c fortsetzt. Der Teil der Röhre mit dem Platinstab wird der zu messenden Hitze ausgesetzt. Der Eisenstab c wirkt auf den kürzern Arm eines Hebels, dessen längerer, mit gezahntem Bogen versehener Arm ein kleines Getriebe mit dem Zeiger d in Bewegung setzt, der auf einem empirisch geteilten Gradbogen die Hitzegrade angibt. Wedgewoods Thonpyrometer beruht auf der Eigenschaft mancher Thonarten, beim Erhitzen zu schwinden; es besteht aus einer Anzahl kleiner Thoncylinder und einer Vorrichtung, die Dicke derselben zu messen. Diese Vorrichtung wird von einer Messingplatte mit zwei Leisten gebildet, deren Abstand an einem Ende 0,5 Zoll (engl.) beträgt und gleichmäßig bis 0,3 Zoll abnimmt, und zwischen denen die Thoncylinder um so weiter hineingeschoben werden können, je mehr sie in der Hitze geschwunden sind. Die ungleiche Zusammenziehung verschiedener Thonarten und die Unregelmäßigkeit des Schwindens, wodurch die Cylinder sich verziehen, hindern jede Genauigkeit. Nach Weinhold sind überhaupt alle P., welche sich auf die Volumveränderungen fester Körper gründen, unzuverlässig. Namentlich gilt dies auch von jenen Metallpyrometern, deren Angaben auf der Formveränderung eines aus zwei verschiedenen Metallen zusammengenieteten Doppelstreifens beruhen, wie z. B. von dem Spiralpyrometer von Öchsle. Bessere Temperaturangaben liefern kalorimetrische Versuche; eine Kugel von Platin oder Eisen (Schmiedeeisen ist dem Platin vorzuziehen) wird, nachdem sie der zu messenden Hitze ausgesetzt worden ist, in eine gewogene Wassermenge gebracht und aus der Temperaturerhöhung der letztern und der spezifischen Wärme der Kugel die gesuchte Temperatur berechnet. Prinsep benutzte zur Beurteilung hoher Wärmegrade die Schmelzpunkte von Metalllegierungen; Goldsilberlegierungen mit regelmäßig steigendem Goldgehalt und Silberplatinlegierungen mit steigendem Platingehalt wurden zu Blech ausgewalzt und kleine Stückchen davon in Grübchen auf eine Thonplatte gelegt. Die Legierungen bilden gleichsam die Skala eines Thermometers, und das successive Schmelzen der Legierungen gibt Anhaltspunkte zur Beurteilung der erreichten Temperatur; von einem eigentlichen Messen der letztern kann aber deswegen nicht die Rede sein, weil die Schmelzpunkte der Legierungen unbekannt und die von Prinsep darüber gemachten Annahmen nicht stichhaltig sind. Das Marmorpyrometer von Lamy beruht auf der Voraussetzung, daß der Druck der Kohlensäure, welche sich in der Hitze durch die Dissoziation des kohlensauren Kalks entwickelt, nur von der Temperatur abhängig sei. Schinz suchte aus der Temperatur an der Außenfläche eines Ofens und aus der Wärmeleitungsfähigkeit des Ofenmaterials die in demselben herrschende Temperatur zu bestimmen. Nachdem schon Pouillet ein thermoelektrisches Element aus Gold und Platin zu pyrometrischen Messungen angewendet (thermoelektrisches P.), glaubte Becquerel mit einem solchen aus Platin und Palladium bessere Resultate zu erzielen, deren Richtigkeit jedoch von Saint-Claire Deville und Troost bestritten wurde. Becquerel suchte ferner die Temperatur glühender undurchsichtiger Körper, wie Platin, Magnesia, Kohle, zu bestimmen, indem er die Intensität des von ihnen ausgestrahlten Lichts bestimmter Farbe (z. B. des roten, durch ein Rubinglas gegangenen) mit einem Polarisationsphotometer (s. Photometrie, S. 27) maß und mittels einer Formel, welche das Ausstrahlungsgesetz ausdrückt, die Temperatur berechnete (optisches P.). Schon Cagniard-Latour hatte die durch Änderung der Schallgeschwindigkeit bedingte Höhenänderung des Tons einer Pfeife zu Temperaturbestimmungen vorgeschlagen; dieses akustische P. wurde neuerdings von Alfred Mayer wieder in Anregung gebracht, jedoch nicht bis zur technischen Brauchbarkeit ausgebildet. Nach Weinhold ist von den fertig zu beziehenden Pyrometern nur das Widerstandspyrometer von Siemens brauchbar und zuverlässig. [487] Dasselbe gründet sich auf die Thatsache, daß der galvanische Widerstand mit der Temperatur wächst, und besteht aus einer Batterie von sechs Leclanché-Elementen (Fig. 3, B), einem Kommutator

| |
| Fig. 3. Siemens’ Widerstandspyrometer. | |
C, zwei Voltametern V und V1 und zwei Widerständen, deren einer N aus Neusilberdraht besteht und die gewöhnliche Temperatur behält, während der andre P, ein auf einen Porzellancylinder gewickelter Platindraht, der zu messenden Temperatur ausgesetzt wird. Die Drahtverbindungen zwischen diesen einzelnen Teilen sind in der schematischen Fig. 3 angedeutet. Die Teile C, N, V, V1 sind auf einem gemeinschaftlichen Stativ befestigt, die drei Leitungsdrähte c, x und x1 in einem Kabel vereinigt. Wenn der Widerstand P durch Erwärmung des Platindrahts zunimmt, so entwickelt sich in dem Voltameter V1 weniger Knallgas als in dem Voltameter V. Bezeichnet man mit und die in den gleichnamigen Voltametern in gleicher Zeit entwickelten Knallgasmengen und mit den der Temperatur (Celsiusgrade) entsprechenden Widerstand der Platinrolle, so ist , und die Temperatur kann nun aus der Formel , worin die absolute Temperatur , (= 10 Siemens-Einheiten) den Widerstand der Platinrolle bei 0° bedeutet und 0,039369, 0,00216407, −0,24127 ist, berechnet oder bequemer aus einer nach dieser Formel berechneten Tabelle entnommen werden. Vgl. Bolz, Die P. (Berl. 1888).













