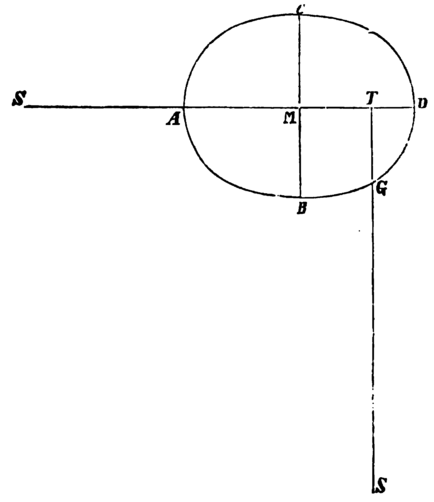
No. 274. S. 444. Es sei ACDB die Mondbahn, T die Erde, A das Apogeum des Mondes, S die Sonne und deren Abstand von T im Mittel ST = a. Die halbe grosse Axe der Mondbahn sei AM = α, ihre halbe kleine MB = β, die Excentricität MT = αε, also AT = α(1 + ε) und SA = a — α(1 + ε). Ferner wird die Ordinate TG = α(1 - ε²) und SG = a — α(1 - ε²) also TG < AT, SG > AS. Wenn daher der Mond sich im Punkte A befindet, wird die Wirkung der Sonne auf ihn grösser sein, wenn die Sonne sich in der Richtung AD befindet, als die von S ausgehende Wirkung auf den in G befindlichen Mond, wenn die Sonne sich in der auf AD senkrechten Richtung TG befindet und zwar verhält sich die erste Anziehung zur zweiten wie .
No. 275. S. 445. Für die Excentricität der Erdbahn = 0,0168 wird der grösste Abstand der Sonne von der Erde = 1,0168, der kleinste = 0,9832; demnach die kleinste Gleichung = = 3' 34,"0, die grösste Gleichung = = 3' 56,"7.
No. 276. S. 445. Der für den mittlern Abstand a geltende Werth von 47" ändert sich in demselben Verhältniss, wie in der vorhergehenden Bemerkung und da die in dieser gefundene Aenderung 11" bei 3' 45" = 225" des mittlern Werthes, also etwa 1/20 letztem beträgt, so muss hier 45" um 2" steigen und sinken.

No. 277. S. 416. Man schlage aus D mit dem Radius DF einen Kreis, alsdann ist E das Apogeum des Mondes und ☾ sein Perigeum. Es sei α das Apogeum der Sonne, P das Perigeum, ☉ der Ort der Sonne.
Nach der Voraussetzung ist dDE = DCB = 2 · ☉E, EDC = 180° — 2 · ☉E, FDE = ☉E — PE. (Voraussetzung im Text), also addirt EDC + FDE = CDF 180° — ☉E = PE. Es ist aber PE☉α = 180°, mithin 180° = ☉E — PE = CDF
Isaac Newton: Mathematische Principien der Naturlehre. Robert Oppenheim, Berlin 1872, Seite 640. Digitale Volltext-Ausgabe bei Wikisource, URL: https://de.wikisource.org/w/index.php?title=Seite:NewtonPrincipien.djvu/648&oldid=- (Version vom 1.8.2018)




