Mathematische Principien der Naturlehre/Buch1-II

← Buch I. Abschnitt I.

Mathematische Principien der Naturlehre (1872) von Isaac Newton, übersetzt von Jakob Philipp Wolfers Buch I. Abschnitt II.

Buch I. Abschnitt III. →

ABSCHNITT II.

Von der Bestimmung der Centripetalkräfte.

---

Fig. 15.

§. 13. Lehrsatz. Wenn Körper sich in Bahnen bewegen, deren Radien stets nach dem unbeweglichen Mittelpunkte der Kräfte gerichtet sind; so liegen die von ihnen beschriebenen Flächen in festen Ebenen und sind den Zeiten proportional.

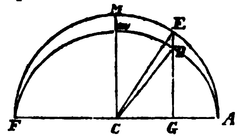
Man theile die Zeit in gleiche Abschnitte, und es beschreibe der Körper, vermöge der ihm beigebrachten Kraft, in dem ersten Zeitabschnitt die gerade Linie AB. Derselbe würde alsdann, wenn nichts ihn verhinderte, (nach 1. Gesetz) in dem zweiten Zeitabschnitt geradlinig nach c fortgehen, dergestalt dass

Bc = AB,

und indem man die Radien AS, BS, cS nach dem Mittelpunkte S der Kräfte zieht,

A.     Δ ASB = BSc

wäre. Ist der Körper aber nach B gekommen, so wirkt die Centripetalkraft mit einem einzigen aber starken Impuls auf ihn und bewirkt, dass er von der geraden Linie Bc abgelenkt wird und längs BC fortgeht. Zieht man nun

cC ∥ BS,

bis cC die Linie BC in C schneidet; so befindet sich der Körper am Ende des zweiten Zeitabschnittes (nach Gesetze, Zusatz 1.) in C und in derselben Ebene mit SAB. Zieht man nun SC, so ist, weil

cC ∥ BS

Δ SBC = SBc,

oben (A.) war

SBc = ASB,

also ist auch

B.     Δ SBC = SAB.

Aus demselben Grunde wirkt die Centripetalkraft nach und nach in den Punkten C, D, E, etc. dergestalt, dass der Körper in den einzelnen Zeitabschnitten bezüglich die Linie CD, DE, etc. beschreibt. Diese liegen alle in derselben Ebene, und es wird

C.	$\scriptstyle {\begin{cases}\Delta \ SCD=SBC.\\\Delta \ SDE=SCD.{\text{ etc.}}\end{cases}}$

In gleichen Zeitabschnitten werden daher gleiche Flächen in der unbewegten Ebene beschrieben, und indem man dieselben zusammensetzt, verhalten sich die Flächen SACS, SAES zu einander, wie die Zeiten, in denen sie beschrieben sind. Vermehrt man nun ins Unendliche die Zahl der Dreiecke und verkleinert man ihre Grundlinien, so wird (nach §. 3., Zusatz 4.) der Umfang ADE eine krumme Linie. Es wirkt daher die Centripetalkraft, durch welche der Körper beständig von der Tangente dieser Curve abgezogen wird, unaufhörlich, und die den Zeiten der Beschreibung proportionalen Flächenräume SABCS und SABCDES werden auch in diesem Falle ihnen proportional bleiben.     W. z. b. w.

Zusatz 1. Die Geschwindigkeiten eines, im nicht widerstehenden Mittel gegen einen unbeweglichen Mittelpunkt gezogenen, Körpers verhalten sich umgekehrt wie die Perpendikel von jenem Mittelpunkte auf die geradlinige Tangente der Bahn. Sie verhalten sich nämlich in A, B, C, D wie die Grundlinien AB, BC, CD, DE, und diese umgekehrt wie die Höhen.

Zusatz 2. Ergänzt man die Sehnen AB und BC der, von demselben Körper im nicht widerstehenden Mittel beschriebenen, Bogen zum Parallelogramm ABCV, und verlängert man die Diagonale BV desselben in derjenigen Lage, welche sie zuletzt hat, wo jene Bogen ins Unendliche vermindert werden; so geht sie durch den Mittelpunkt der Kräfte.^[1]

Zusatz 3. Werden die Sehnen AB und BC, so wie DE und EF von Bogen, die in gleichen Zeiten beschrieben sind, zu Parallelogrammen ABCV und DEFZ ergänzt, so stehen die Kräfte in B und E zu einander im letzten Verhältniss der Diagonalen BV und EZ, wenn jene Bogen unendlich klein werden. Die Bewegungen BC und EF des Körpers werden nämlich (nach Gesetze, Zusatz 1.) respective aus den Bewegungen Bc und BV, Ef und EZ zusammengesetzt und die Bewegungen BV = Cc und EZ = Ff nach dem Beweise dieses §. durch den Impuls der Centripetalkraft in B und C erzeugt; daher werden sie diesen Impulsen proportional sein.

Zusatz 4. Die Kräfte, durch welche beliebige Körper in nicht widerstehenden Mitteln von der geradlinigen Bewegung abgezogen und in krumme Bahnen gebracht werden, verhalten sich zu einander, wie die Sinus versus der in gleichen Zeiten beschriebenen Bogen, welche Sinus versus nach dem Mittelpunkte der Kräfte zu convergiren und die Sehnen halbiren, wenn jene Bogen ins Unendliche vermindert werden. Diese Sinus versus sind nämlich die Hälften der Diagonalen, von denen im Zusatz 3 die Rede war.

Zusatz 5. Dieselben Kräfte verhalten sich zur Kraft der Schwere wie diese Sinus versus zu den auf den Horizont perpendikulären Höhen parabolischer Bogen, welche Geschosse in derselben Zeit beschreiben.

Zusatz 6. Alles dieses gilt, nach Gesetze, Zusatz 5., auch dann wenn die Ebenen, in denen die Körper sich bewegen, zugleich mit dem in ihnen befindlichen Centrum nicht ruhen, sondern sich gleichförmig und geradlinig bewegen.

§. 14. Lehrsatz. Jeder Körper, welcher sich in irgend einer Curve bewegt, deren Radien nach einem, entweder ruhenden oder gleichförmig und geradlinig fortschreitenden, Punkte gerichtet sind und um denselben der Zeit proportionale Räume beschreibt, wird durch eine, nach jenem Punkte gerichtete, Centripetalkraft angetrieben.

1. Fall. Jeder Körper, welcher sich in einer Curve bewegt, wird (nach 1. Gesetz) durch irgend eine auf ihn einwirkende Kraft vom geradlinigen Wege abgebracht. Jene Kraft aber, durch welche dies geschieht und der Körper gezwungen wird, die sehr kleinen und in gleichen Zeiten gleiche Dreiecke

SAB, SBC, SCD, SDE, etc.

um den unbeweglichen Punkt S zu beschreiben, wirkt im Punkte B längs einer cC parallelen Linie (nach Elemente, Buch I., Satz 40. und 2. Gesetz), d. h. längs der Linie BS^[2]; im Orte C längs einer dD parallelen Linie, d. h. längs der Linie CS u. s. w. Sie wirkt also immer längs solcher Linien, welche nach jenem unbeweglichen Punkte S gerichtet wird. Figur 15.     W. z. b. w.

2. Fall. Nach Gesetze, Zusatz 5. ist es gleichgültig, ob die Fläche, in welcher der Körper die krummlinige Figur beschreibt, ruhet oder ob sie zugleich mit dem Körper, der beschriebenen Figur und ihrem Punkte S sich gleichförmig und geradlinig fortbewegt.

Zusatz 1. Sind in nicht widerstehenden Mitteln die beschriebenen Flächenräume den Zeiten nicht proportional, so sind auch die Kräfte nicht nach dem Durchschnittspunkte der Radien gerichtet, und zwar weichen sie nach der Richtung davon ab, wohin die Bewegung geschieht, wenn diese beschleunigt, hingegen rückwärts, wenn sie verzögert wird.

Zusatz 2. In allen auch widerstehenden Mitteln sind die Kräfte wenn die Beschreibung der Flächenräume beschleunigt wird, nicht nach dem Durchschnittspunkte der Radien gerichtet, sondern weichen in einer vorwärtsliegenden Richtung davon ab.

§. 15. Anmerkung. Der Körper kann durch eine Centripetalkraft angetrieben werden, die aus mehreren einzelnen Kräften zusammengesetzt ist. In diesem Falle ist der Satz so zu verstehen, dass jene, aus allen einzelnen zusammengesetzte Kraft nach dem Punkte S gerichtet ist.

Wirkt ferner irgend eine Kraft beständig nach einer, auf die beschriebene Oberfläche perpendikulären, Richtung, so wird dieselbe bewirken, dass der Körper aus der Ebene seiner Bahn abgelenkt wird; aber die Grösse der beschriebenen Fläche wird sie weder vermehren noch vermindern und daher bei der Zusammensetzung der Kräfte vernachlässigt werden können.

§. 16. Lehrsatz. Jeder Körper, welcher mit einem, nach dem Mittelpunkte eines andern irgendwie sich bewegenden Körpers gezogenen Radius um jenen Punkt Flächen beschreibt, welche der Zeit proportional sind, wird durch eine Kraft angetrieben, die aus der nach dem andern Körper gerichteten Centripetalkraft, und der ganzen beschleunigenden den andern antreibenden, Kraft zusammengesetzt ist.

Werden nämlich beide Körper L und T durch eine neue Kraft, welche derjenigen gleich und entgegengesetzt ist, durch die der zweite angetrieben wird, nach parallelen Richtungen angetrieben; so wird (nach Gesetze, Zusatz 6.) der erste Körper L fortfahren, dieselben Flächen wie vorher um den zweiten T zu beschreiben. Die Kraft aber, welche T antrieb, wird jetzt durch die ihr gleiche und entgegengesetzte aufgehoben, und desshalb wird (nach 1. Gesetz) jener zweite Körper T, sich selbst überlassen, entweder ruhen, oder sich gleichförmig und geradlinig fortbewegen, und der erste L, angetrieben durch den Unterschied der Kräfte fortwährend der Zeit proportionale Flächen um den zweiten T beschreiben. Nach §. 14. ist daher der Unterschied der Kräfte nach jenem zweiten Körper T als Centrum gerichtet.

Zusatz 1. Beschreibt ein Körper L mit einem, nach einem zweiten T gezogenen, Radius der Zeit proportionale Flächenräume, und zieht man von der ganzen Kraft (mag sie eine einfache oder nach Gesetze, Zusatz 2. aus mehrern zusammengesetzte sein), welche den ersten Körper L antreibt, nach dem eben erwähnten Zusatze die ganze beschleunigende Kraft ab, welche den zweiten Körper T antreibt; so strebt die ganze übrig bleibende Kraft nach dem letztern als dem Centrum.

Zusatz 2. Sind die Flächen so nahe als möglich der Zeit proportional, so ist die übrigbleibende Kraft auch so nahe als möglich nach dem zweiten Körper T gerichtet.

Zusatz 3. Ist umgekehrt die übrig bleibende Kraft möglichst nahe nach dem zweiten Körper T gerichtet, so sind die beschriebenen Flächenräume möglichst nahe der Zeit proportional.

Zusatz 4. Beschreibt ein Körper L mit einem, nach einem zweiten T gezogenen, Radius Flächen, welche verglichen mit den Zeiten sehr ungleich sind, und ruht entweder der zweite Körper T oder bewegt er sich gleichförmig und geradlinig fort; so ist die Wirkung der nach dem letztern gerichteten Centripetalkraft entweder = 0, oder vermischt und zusammengesetzt mit sehr starken Wirkungen anderer Kräfte, und die ganze, aus allen (wenn deren mehrere vorhanden sind) zusammengesetzte Kraft ist nach einem andern unbeweglichen oder beweglichen Centrum gerichtet, um welche die Beschreibung der Flächen gleichförmig erfolgt. Dasselbe ist der Fall, wenn der zweite Körper T sich auf eine beliebige Weise bewegt; wofern man nur als Centripetalkraft diejenige Kraft annimmt, welche man nach Abzug der ganzen auf T wirkenden erhält.

§. 17. Anmerkung. Die gleichförmige Beschreibung der Flächen giebt das Centrum an, nach welchem die am stärksten auf den Körper wirkende Kraft gerichtet ist, und man sagt mit Recht, dass jede kreisförmige Bewegung um denjenigen Mittelpunkt stattfinde, durch dessen Kraft der Körper von der geradlinigen Bewegung abgezogen und in seiner Bahn erhalten wird. Warum sollten wir nun nicht in der Folge die gleichförmige Beschreibung der Flächen als Kennzeichen eines Mittelpunktes annehmen, um welchen jede kreisförmige Bewegung im freien Raume stattfindet?

§. 18. Lehrsatz. Die Centripetalkräfte solcher Körper, welche verschiedene Kreise mit gleichförmiger Bewegung beschreiben, sind nach den Mittelpunkten dieser Kreise gerichtet, und verhalten sich zu einander direct wie die Quadrate gleichförmig beschriebener Bogen und indirect wie die Radien.

Diese Kräfte sind, nach §. 14. und §. 13., Zusatz 2., nach den Mittelpunkten gerichtet und verhalten sich zu einander, wie die Sinus versus der in den kleinsten gleichen Zeiten beschriebenen Bogen (nach §. 13., Zusatz 4.), d. h. wie die Quadrate jener Bogen, dividirt durch die Durchmesser der Kreise (nach §. 7.). Da nun diese Bogen sich wie die in beliebigen gleichen Zeiten beschriebenen Bogen und die Durchmesser sich wie ihre Radien verhalten; so werden die Kräfte den Quadraten beliebiger gleichzeitig beschriebener Bogen, durch die Radien der Kreise dividirt, proportional sein.     W. z. b. w.

Zusatz 1. Da die Bogen den Geschwindigkeiten proportional sind, so verhalten sich die Centripetalkräfte, wie die Quadrate der Geschwindigkeiten, dividirt durch die Radien der Kreise.

Zusatz 2. Da die Umlaufszeiten im zusammengesetzten directen Verhältniss der Radien und indirecten der Geschwindigkeiten stehen, so verhalten sich die Centripetalkräfte indirect wie die Quadrate der Umlaufszeiten und direct wie die Radien^[3].

Zusatz 3. Sind die Umlaufszeiten einander gleich, so verhalten sich sowohl die Centripetalkräfte, als auch die Geschwindigkeiten wie die Radien; und umgekehrt.

Zusatz 4. Verhalten sich die Quadrate der Umlaufszeiten und der Geschwindigkeiten wie die Radien, so sind die Centripetalkräfte einander gleich; und umgekehrt.

Zusatz 5. Sind die Umlaufszeiten den Radien proportional, so verhalten sich die Centripetalkräfte indirect wie die Radien; und umgekehrt.

Zusatz 6. Sind die Quadrate der Umlaufszeiten den Cuben der Radien proportional, so verhalten sich die Centripetalkräfte indirect wie die Quadrate der Radien, die Geschwindigkeiten aber indirect wie die Quadratwurzeln der Radien; und umgekehrt^[4].

Zusatz 7. Ist allgemein die Umlaufszeit proportional

Rⁿ,

wo n eine beliebige Zahl bezeichnet; so wird die Geschwindigkeit sich indirect verhalten wie

R^n–1,

und die Centripetalkraft indirect wie

R^2n–1.

Zusatz 8. Alles Bisherige gilt auch von den Zeiten, Geschwindigkeiten und Kräften, womit Körper ähnliche Theile ähnlicher Figuren, deren Mittelpunkte ähnlich liegen, beschreiben, und es folgt dies aus der Anwendung der vorhergehenden Beweise auf diesen Fall. Man macht diese Anwendung, indem man eine sich gleichbleibende Beschreibung der Flächen statt der gleichförmigen Bewegung, und die Abstände der Körper vom Mittelpunkte statt der Radien annimmt.

Zusatz 9. Aus demselben Beweise folgt auch, dass der Bogen, welchen ein Körper in einem, unter Einwirkung einer gegebenen Centripetalkraft gleichförmig beschriebenen, Kreise während einer gegebenen Zeit zurücklegt, die mittlere Proportionale zwischen dem Durchmesser des Kreises und der Höhe ist, um welche der Körper während derselben Zeit und vermöge derselben Kraft herunterfallen würde^[5].

§. 19. Anmerkung. Der Fall des Zusatzes 6. findet bei der Bewegung der Himmelskörper statt (wie Wren, Hook und Halley ursprünglich gefunden haben), wesshalb ich dasjenige, was sich auf die Abnahme der Centripetalkräfte im doppelten Verhältniss der Radien bezieht, im Folgenden näher auseineindersetzen werde.

Ferner kann man mittelst des vorhergehenden Lehrsatzes und seiner Zusätze auch auf das Verhältniss der Centripetalkraft zu jeder bekannten Kraft schliessen, wie z. B. zur Kraft der Schwere. Denn wenn der Körper sich auf einem um die Erde concentrischen Kreise vermöge seiner Schwere bewegt, so ist die letztere seine Centripetalkraft. Aus dem Falle der Körper wird aber nach §. 18., Zusatz 9. so wohl die Umlaufszeit, als auch der in jeder Zeit beschriebene Bogen bekannt. Durch derartige Sätze hat Huygens in seinem vortrefflichen Werke über Pendeluhren die Kraft der Schwere mit den Centrifugalkräften umlaufender Körper verglichen.

Das Vorhergehende kann auch auf folgende Weise erwiesen werden. Man denke sich in einem Kreise ein Vieleck von beliebig vielen Seiten beschrieben. Wird nun ein Körper bei seiner Bewegung längs der Seiten an den einzelnen Ecken durch den Kreis zurückgeworfen, so verhält sich die Kraft, mit welcher er bei den einzelnen Zurückwerfungen auf den Kreis wirkt, wie seine Geschwindigkeit. Die Summe der Kräfte in einer gegebenen Zeit verhält sich daher zusammengesetzt, wie jene Geschwindigkeit und die Anzahl der Zurückwerfungen, d. h. wenn das Polygon seiner Art nach gegeben ist, wie der in der gegebenen Zeit beschriebene Weg und derselbe Weg, dividirt durch den Radius des Kreises. Demnach verhält sich die Summe wie das Quadrat seines Weges, dividirt durch den Radius. Fällt nun das Polygon, durch unendliche Verkleinerung seiner Seiten, mit dem Kreise zusammen, so verhält sich die Summe wie das Quadrat des Bogens, dividirt durch den Radius. Diese Summe ist aber die Kraft, mit welcher der Körper auf den Kreis wirkt, und gleich und entgegengesetzt ist ihr diejenige Kraft, mit welcher der Kreis den Körper beständig gegen den Mittelpunkt zurückstösst.

§. 20. Aufgabe. Die Geschwindigkeit, mit welcher ein Körper eine gegebene Figur in Folge von Kräften beschreibt, welche nach einem gemeinschaftlichen Centrum gerichtet sind, ist für beliebige Orte gegeben; man soll das Centrum finden.

Die beschriebene Figur werde durch drei Tangenten pT, TQV und VR in den Punkten P, Q und R berührt, und es mögen sich jene in den Punkten T und V schneiden. Man errichte in den Berührungspunkten Perpendikel PA, QB und RC auf die Tangenten, welche den Geschwindigkeiten in diesen Punkten bezüglich umgekehrt proportional sind. Es verhält sich also, wenn wir die Geschwindigkeit in P, Q, R, respective durch φ(P), φ(Q), φ(R) bezeichnen,

φ(Q) : φ(P) = PA : QB

φ(R) : φ(Q) = QB : RC.

Durch die Endpunkte A, B und C ziehe man

AD ∥ PT

CE ∥ RV;

alsdann werden die Linien TD und VE verlängert, sich in dem gesuchten Centrum schneiden.

Fig. 17.

Die vom Mittelpunkt S auf die Tangenten PT und QT gefällten Perpendikel verhalten sich nämlich (nach §. 13., Zusatz 1.) indirect wie die Geschwindigkeiten des Körpers in den Punkten P und Q, und daher direct wie

AP : BQ

d. h. wie die vom Punkte D auf die Tangenten gefällten Perpendikel

DP' : DQ'.

Hieraus schliesst man leicht, dass die Punkte S, D, T in einer geraden Linie liegen.^[6] Ebenso wird bewiesen, dass S, E, V in einer geraden Linie liegen; daher muss das Centrum S sich im Durchschnittspunkte beider Linien befinden.     W. z. b. w.

Fig. 18.

§. 21. Lehrsatz. Ein Körper bewegt sich in nicht widerstehendem Mittel um ein unbewegliches Centrum und in einer beliebigen Bahn; er beschreibt in einer sehr kurzen Zeit irgend einen eben entstehenden Bogen, dessen Pfeil Pv man gezogen hat und welcher letztere die Sehne des Bogens halbirt und verlängert durch das Centrum der Kräfte geht. Alsdann verhält sich die Centripetalkraft in der Mitte des Bogens direct wie jener Pfeil und indirect wie das Quadrat der Zeit. Setzt man also die zur Beschreibung des Bogens QPq erforderliche Zeit = t, so ist jene Kraft proportional

$\scriptstyle {\frac {Pv}{t^{2}}}$.

Es verhält sich nämlich in einer gegebenen Zeit (nach §. 13., Zusatz 4.) Pv wie die Kraft, und es wächst der Bogen in demselbem Verhältniss, in welchem die Zeit zunimmt; hingegen wächst (nach §. 11., Zusatz 2 und 3.) der Pfeil Pv im doppelten Verhältniss der Zeit; er ist also der Kraft und dem Quadrate der Zeit proportional. Umgekehrt verhält sich die Kraft also direct wie der Pfeil Pv und indirect wie das Quadrat der Zeit. Dasselbe wird auch leicht durch den §. 10., Zusatz 4. bewiesen.

Zusatz 1. Ein Körper P beschreibt, indem er sich um das Centrum S bewegt, eine Curve APQ und die gerade Linie ZPR berührt dieselbe im Punkte P. Zieht man nun von einem andern unbestimmten Punkte Q

QR ∥ SP

und QT perpendikulär auf SP; so verhält sich die Centripetalkraft indirect wie Körper

$\scriptstyle {\frac {SP^{2}\ \cdot \ QT^{2}}{QR}}$,

wobei in diesem Körper immer der letzte Werth genommen werden muss, welchen er vor dem Zusammenfallen der Punkte P und Q erlangt.

Es ist nämlich

QR = Pv,

d. h. dem Pfeile des verdoppelten Bogens PQ, in dessen Mitte P liegt.

Das doppelte Dreieck

SQP = SP · QT

ist der Zeit proportional, in welcher jener verdoppelte Bogen PQ beschrieben wird und kann daher als die Zeit vertretend betrachtet werden.^[7]

Zusatz 2. Ist SY perpendikulär auf die Tangente PR gezogen, so wird die Centripetalkraft sich indirect verhalten wie der Körper

$\scriptstyle {\frac {SY^{2}\ \cdot \ QP^{2}}{QR}}$:

es ist nämlich (für den verschwindenden Bogen)

SY · QP = SP · QT.

Zusatz 3. Ist die Bahn entweder selbst ein Kreis, oder berührt oder schneidet sie denselben concentrisch, d. h. hat sie einen möglichst kleinen Berührungs- oder Durchschnittswinkel mit dem Kreise, dieselbe Krümmung und denselben Krümmungshalbmesser in P; ist PV die Sehne dieses Kreises, welche vom Körper durch das Centrum der Kräfte gezogen ist: so verhält sich die Centripetalkraft indirect wie der Körper

SY² · PV.

Es ist nämlich

$\scriptstyle PV={\frac {QP^{2}}{QR}}$^[8].

Zusatz 4. Unter denselben Voraussetzungen verhält sich die Centripetalkraft direct wie das Quadrat der Geschwindigkeit und indirect wie das Perpendikel SY (nach § 13. Zusatz 1.).

Zusatz 5. Ist irgend eine krummlinige Figur APQ, und in ihr ein Punkt S gegeben, nach welchem die Centripetalkraft beständig gerichtet ist; so kann man das Gesetz der letztern finden, vermöge welches ein Körper P, vom gradlinigen Wege stets abgezogen, auf dem Umfange jener Figur festgehalten wird und sich auf demselben bewegt. Man hat zu diesem Ende den Körper

$\scriptstyle {\frac {SP^{2}\ \cdot \ QT^{2}}{QR}}=SY^{2}\ \cdot \ PV$

zu berechnen, welcher dieser Kraft indirect proportional ist. Die folgenden Aufgaben enthalten Beispiele hiervon.

§. 22. Aufgabe. Es bewegt sich ein Körper auf der Peripherie eines Kreises; man sucht das Gesetz der Centripetalkraft, welche nach irgend einem Punkte gerichtet ist.

Fig. 19.

Es sei VQPA die Peripherie des Kreises, S das Centrum der Centripetalkraft, in P befinde sich der auf der Peripherie fortschreitende Körper und Q der nächste von ihm zu erreichende Ort desselben. Man ziehe die Tangente PRZ des Kreises in P durch S die Sehne VP, den Durchmesser VA und die Verbindungslinie AP. Fällt man nun

PK	perpendikulär	auf	VA
QT	„	„	VP,

zieht man durch Q LR ∥ VP, welche erstere Linie den Kreis in L und die Tangente PR in R schneidet, schneiden sich ferner QT und PR verlängert in Z; so ist

Δ ZQR ∼ ZTP ∼ VPA,

also

RP² : QT² = VA² : VP².

Ferner ist

RP² = RQ · RL,

daher

$\scriptstyle QT^{2}={\frac {RQ\ \cdot \ RL\ \cdot \ VP^{2}}{VA^{2}}}$.

Multiplicirt man diese Gleichung auf beiden Seiten durch

$\scriptstyle {\frac {SP^{2}}{QR}}$,

so wird

$\scriptstyle {\frac {QT^{2}\cdot \ SP^{2}}{QR}}={\frac {SP^{2}\cdot \ VP^{2}\cdot RL}{VA^{2}}}$,

und da beim Zusammenfallen der Punkte P und Q

RL=VP

wird,

$\scriptstyle {\frac {QT^{2}\cdot \ SP^{2}}{QR}}={\frac {SP^{2}\cdot \ VP^{3}}{VA^{2}}}$.

Nach §. 21., Zusatz 1. und 5. ist daher die Centripetalkraft indirect proportinal

$\scriptstyle {\frac {SP^{2}\cdot \ VP^{3}}{VA^{2}}}$

oder, weil der Durchmesser VA constant ist, indirect proportional

SP² · VP³.

Zweiter Beweis. Man fälle auf die Tangente PR das Perpendikel SY, alsdann wird, weil

Δ SYP ∼ ZTP ∼ VPA

AV : VP = SP : SY

also

$\scriptstyle SY={\frac {VP\ \cdot \ SP}{AV}}$,

und

$\scriptstyle {\frac {SP^{2}\ \cdot \ VP^{3}}{AV^{2}}}=SY^{2}\cdot VP$.

Nach §. 21., Zusatz 3. und 5. ist daher die Centripetalkraft indirect proportional

$\scriptstyle {\frac {SP^{2}\ \cdot \ VP^{3}}{AV^{2}}}$ oder SP² · VP³, weil AV constant ist.

Fig. 20.

Zusatz 1. Fällt der Punkt S nach welchem die Centripetalkraft stets gerichtet ist, auf die Peripherie des Kreises in V, so ist die Centripetalkraft indirect proportional

SP⁵.

Zusatz 2. Die Kraft, vermöge welcher der Körper P sich auf dem Kreise APTV um das Centrum S herumbewegt, verhält sich zu der Kraft, vermöge welcher derselbe Körper auf demselben Kreise und in derselben Umlaufszeit sich um ein beliebiges anderes Centrum R bewegen kann, wie

RP² · SP : SG³,

wo SG von S nach der Tangente PG ∥ RP ist.

Nach diesem Paragraph verhält sich nämlich die erste Kraft zur zweiten, wie

RP² · PT³ : SP² · PV³

d. h. wie

SP · PR² : $\scriptstyle {\frac {SP^{3}\cdot \ PV^{3}}{PT^{3}}}$.

Da aber

Δ PGS ∼ PTV

also

PT : PV = PS : SG;

so wird

$\scriptstyle {\frac {SP^{3}\cdot \ PV^{3}}{PT^{3}}}=SG^{3}$.

Zusatz 3. Die Kraft, vermöge welcher der Körper sich in einer beliebigen Bahn um das Centrum S bewegt, verhält sich zu der, bei derselben Bahn und Verlaufszeit dem Centrum R entsprechenden Kraft, wie

SP · PR² : SG³.

Es bedeuten dabei SP, PR und SG dasselbe in der beliebigen Bahn, wie hier im Kreise. Die Kräfte in der beliebigen Bahn sind nämlich dieselben, wie in einem Kreise von gleicher Krümmung.

Fig. 21.

§. 23. Aufgabe. Ein Körper bewegt sich auf dem Kreise PQA; man sucht das Gesetz der Centripetalkraft, welche nach einem so entfernten Punkte S gerichtet ist, dass man alle nach demselben gezogenen Linien PS und RS als einander parallele ansehen kann.

Man ziehe vom Mittelpunkte C des Kreises den Halbmesser CA, welcher jene Parallelen senkrecht in M und N schneidet und verbinde C mit P.

Da

Δ CPM ∼ TPZ

und nach §. 8.

Δ CPM ∼ TPQ,

so hat man

CP² : PM² = PQ² : QT²

und nach §. 7.

CP² : PM² = PR² : QT².

Ferner ist auch der Natur des Kreises

PR² = QR (RN + QN).

Im Fall, dass die Punkte Q und P zusammenfallen, wird aber

RN + QN = 2PM,

mithin in diesem Falle

CP² : PM² = 2PM · QR : QT²

und

$\scriptstyle {\frac {QT^{2}}{QR}}={\frac {2PM^{3}}{CP^{2}}}$

endlich,

$\scriptstyle {\frac {QT^{2}\cdot \ SP^{2}}{QR}}={\frac {2PM^{3}\cdot \ SP^{2}}{CP^{2}}}$.

Nach §. 21., Zusatz 1. und 5. ist daher die Centripetalkraft indirect proportional

$\scriptstyle {\frac {2PM^{3}\cdot \ SP^{2}}{CP^{2}}}$ oder PM³,

weil $\scriptstyle {\frac {2SP^{2}}{CP^{2}}}$ constant ist.

Denselben Schluss zieht man leicht aus §. 22.

§. 24. Anmerkung. Auf wenig verschiedene Weise zeigt man, dass ein Körper sich in einer Ellipse, Parabel oder Hyperbel bewegt, in Folge einer Centripetalkraft, welche indirect der nach einem sehr entfernten Centrum der Kräfte gerichteten Ordinate proportional ist.

Fig. 22.

§. 25. Aufgabe. Ein Körper bewegt sich auf der Spirallinie PQ, welche alle Radien SP, SQ etc. unter einem constanten Winkel schneidet; man sucht das Gesetz der nach dem Centrum S der Spirallinie gerichteten Centripetalkraft. Ist der unbestimmt kleine Winkel PSQ gegeben, so kennt man wegen der übrigen bekannten Winkel, die Figur SPRQT ihrer Form nach. Das Verhältniss $\scriptstyle {\frac {QT}{QR}}$ ist daher gegeben und, weil jene Figur der Form nach gegeben ist, $\scriptstyle {\frac {QT^{2}}{QR}}$ proportional QT, d. h. SP.

Verändert man nun den Winkel PSQ, so ändert sich die Linie QR, welche den Berührungswinkel QPR unterspannt, nach §. 11. im doppelten Verhältniss von PR oder QT. Daher ist das Verhältniss

$\scriptstyle {\frac {QT^{2}}{QR}}$

constant und gleich SP, so wie

$\scriptstyle {\frac {QT^{2}\cdot \ SP^{2}}{QR}}$ proportional SP³,

d. h. nach §. 21., Zusatz 1. und 5. indirect proportional der Centripetalkraft.

Zweiter Beweis. Das auf die Tangente gefällte Perpendikel SY und die Sehne PV desjenigen Kreises, welcher die Spirale concentrisch schneidet, stehen zum Radius SP im constanten Verhältniss; daher ist SP³ proportional SY² · PV, d. h. nach §. 21., Zusatz 3. und 5. indirect proportional der Centripetalkraft.

§. 26. Lehnsatz. Alle um eine gegebene Ellipse beschriebenen Parallelogramme sind einander gleich. Dasselbe gilt von den Parallelogrammen, welche in der Hyperbel an ihre Durchmesser beschrieben werden. Beides ist aus der Lehre von den Kegelschnitten bekannt.^[9]

Fig. 23.

§. 27. Aufgabe. Ein Körper bewegt sich in einer Ellipse; man sucht das Gesetz der nach dem Mittelpunkte der Ellipse gerichteten Centripetalkraft.

Es seien CA und CB die halben Axen der Ellipse, GP und DK conjugirte Durchmesser, PF und QT Perpendikel auf die letztere, Qv die Ordinate des Punktes Q in Bezug auf GP als Abscissenaxe. Vollendet man das Parallelogramm QvPR, so ist nach den Lehren der Kegelschnitte

A.

Pv · vG : Qv² = PC² : CD²^[10].

Da aber

Δ QvT ∼ PCF,

ist B.

Qv² : QT² = PC² : PF²,

und indem man beide Proportionen mit einander verbindet,

C.

Pv · vG : QT² = PC² : CD² · PF²

oder D.

$\scriptstyle vG:{\frac {QT^{2}}{Pv}}=PC^{2}:{\frac {CD^{2}\cdot \ PF^{2}}{PC^{2}}}$.

Nach §. 26. ist ferner E.

$\scriptstyle {\begin{cases}CD\ \cdot \ &PF=BC\ \cdot \ CA\\&Pv=QR\end{cases}}$,

und im Fall die Punkte P und Q zusammenfallen,

F.

vG = 2 · PC.

Substituirt man diese verschiedenen Werthe E. und F. in D., so erhält man

G.

$\scriptstyle {\frac {QT^{2}\cdot \ PC^{2}}{QR}}={\frac {2BC^{2}\cdot \ CA^{2}}{PC}}$.

Nach §. 21., Zusatz 5. ist daher die Centripetalkraft indirect

$\scriptstyle {\frac {2BC^{2}\cdot \ CA^{2}}{PC}}$,

d. h. weil 2BC² · CA² constant ist, indirect $\scriptstyle {\frac {1}{PC}}$ oder direct PC proportional.

Zweiter Beweis. Auf der Linie PQ nehme man, auf der T entgegengesetzten Seite einen Punkt u so an, dass

Tu = Tv

und den Punkt V dergestalt an, dass

uV : vG = DC² : PC²

sei. Da nun nach der Lehre von den Kegelschnitten

Qv² : Pv · vG = DC² · PC²,

so wird

uV : vG = Qv² : Pv · vG

oder

Qv² = Pv · uV.

Addirt man zur letzten Gleichung auf beiden Seiten

uP · Pv = uP · Pv,

so wird

VP · Pv = PQ²^[11].

Demnach wird der Kreis, welcher den Kegelschnitt in P berührt, und durch Q geht, auch durch V gehen. Fallen nun P und Q zusammen, so geht das Verhältniss

uV : vG, welche = DC² : PC² ist,

über in

PV : PG oder PV : 2PC.

Wir erhalten demnach

PV : 2PC = DC² : CP²

und

$\scriptstyle PV={\frac {2DC^{2}}{PC}}$.

Die Kraft, vermöge welcher der Körper P sich in der Ellipse bewegt, ist daher (nach §. 21., Zusatz 3.) indirect

$\scriptstyle {\frac {2DC^{2}\cdot \ PF^{2}}{PC}}$^[12],

d. h. weil 2DC² · PF² constant ist,

PC

direct proportional.

Zusatz 1. Es ist daher die Kraft dem Abstande des Körpers vom Mittelpunkte der Ellipse proportional, und eben so wird, wenn die Kraft dem Abstände von ihrem Centrum proportional ist, der Körper sich auf einer Ellipse bewegen, deren Mittelpunkt mit dem Centrum der Kräfte identisch, oder vielleicht auf einem Kreise, in welchen die Ellipse übergehen kann.

Zusatz 2. Es werden die Umlaufszeiten aller um dasselbe Centrum beschriebenen Ellipsen einander gleich sein. Jene Zeiten sind nämlich bei ähnlichen Ellipsen gleich, nach §. 18., Zusatz 3. und 8. Bei Ellipsen aber, welche eine gemeinschaftliche grosse Axe haben, verhalten sich die Umlaufszeiten direct wie die ganzen Flächenräume und indirect wie gleichzeitig beschriebene Theile derselben, d. h. direct wie die kleinen Axen, und indirect wie die Geschwindigkeiten der Körper am Ende der grossen Axen, oder direct wie die kleinen Axen und indirect wie die, auf die grosse Axe als Abscissenaxe bezogenen, Ordinaten, mithin wegen der Gleichheit des directen und des indirecten Verhältnisses, wie

1 : 1.^[13]

§. 28. Anmerkung. Wird die Ellipse durch Entfernung ihres Mittelpunktes ins Unendliche in eine Parabel verwandelt, so bewegt sich der Körper auf dieser, und es wird die jetzt nach dem unendlich entfernten Punkt Centrum gerichtete Kraft constant. Dies ist Galilei’s Lehrsatz.

Verwandelt sich der parabolische Schnitt (durch Veränderung der Neigung der schneidenden Ebene) in eine Hyperbel, so bewegt sich der Körper auf dem Umfange der letztern, indem die Centripetalkraft in eine Centrifugalkraft übergeht. Sowie in einem Kreise oder einer Ellipse bei denen die Kräfte nach einem, auf einer Abscisse gelegenen Mittelpunkte der Figur gerichtet sind, diese Kräfte, durch Vergrösserung oder Verkleinerung der Ordinaten in irgend einem gegebenen Verhältniss, oder auch durch Aenderung des Neigungswinkels der Ordinaten gegen die Abscisse, immer im Verhältniss der Entfernungen vom Centrum wachsen oder abnehmen, wenn nur die Umlaufszeiten gleich bleiben; werden in allen Figuren, wenn die Ordinaten in irgend einem Verhältniss zu- oder abnehmen, oder der Coordinatenwinkel bei unveränderter Umlaufszeit irgendwie verändert wird, die nach einem beliebigen, auf einer Abscisse gelegenen Centrum, gerichteten Kräfte in den einzelnen Ordinaten im Verhältniss der Abstände vom Centrum zu- oder abnehmen.

Bemerkungen und Erläuterungen [des Übersetzers]

1. No. 4. S. 56. (Dortige Figur). Da nämlich CV ∥ AB und Cc ∥ BV, so ist CVBc ein Parallelogramm, also CV = Bc = AB, und da auch CV ∥ AB, so wird ABCV ebenfalls ein Parallelogramm, dessen Diagonale BV nach der Construction den Mittelpunkt S trifft.
2. No. 5. S. 57. Da AB = BG ist, hat man Δ SAB = SBc. Nach der Voraussetzung ist SAB = SBC, also SBC = SBc, mithin Cc ∥ SB. Längs BS muss auch die Centripetalkraft gerichtet sein, welche bewirken soll, dass der Körper, statt von B längs Bc fortzugehen, nach C hin abgesenkt werde.
3. No. 6. S. 59. Setzt man die Umlaufszeiten in zwei Kreisen = T, t, die Radien = R, r; so würden die in der Zeiteinheit beschriebenen Bogen $\scriptstyle A={\frac {2R\pi }{T}}$, $\scriptstyle a={\frac {2r\pi }{t}}$. Das in §. 18. enthaltene Verhältniss $\scriptstyle {\frac {A^{2}}{R}}:{\frac {a^{2}}{r}}$ geht daher über $\scriptstyle {\frac {4R^{2}\pi ^{2}}{T^{2}R}}:{\frac {4r^{2}\pi ^{2}}{t^{2}r}}={\frac {R}{T^{2}}}:{\frac {r}{t^{2}}}$.
4. No. 7. S. 60. Werden die Centripetalkräfte durch F, f, die Geschwindigkeiten durch V, v bezeichnet; so ist nach dem Lehrsatz und nach Zusatz 2. $\scriptstyle F:f={\frac {R}{T^{2}}}:{\frac {r}{t^{2}}}$ und da hier T²:t² = R³:r³; so wird $\scriptstyle F:f={\frac {1}{R^{2}}}:{\frac {1}{r^{2}}}$. Ferner geht die Proportion $\scriptstyle V:v={\frac {2R\pi }{T}}:{\frac {2r\pi }{t}}$ hier über in $\scriptstyle V:v={\frac {R}{R^{\frac {3}{2}}}}:{\frac {r}{r^{\frac {3}{2}}}}={\frac {1}{R^{\frac {1}{2}}}}:{\frac {1}{r^{\frac {1}{2}}}}$.
5. No. 8. S. 60. Setzt man allgemein die Schwerkraft = 2g, so wird bekanntlich ein vermöge derselben beschriebener Weg f = gt³. Setzt man nun die Zeit t = 1, und wird während derselben Zeit der Bogen a des Kreises beschrieben, so gehört zu demselben die Fallhöhe g und es ist daher g · 2r = a² oder 2g = $\scriptstyle {\frac {a^{2}}{r}}$, d. h. die Schwerkraft identisch mit der Centripetalkraft. Demnach $\scriptstyle f={\frac {a^{2}}{2r}}\cdot t^{2}$ und für t = 1 a² = 2r · f.
6. 

   Fig. 225.

   No. 9. S. 61. Bezeichnet Pp die Geschwindigkeit in P, Qq die Geschwindigkeit in q, wobei die kleinen Stücke Pp und Qq der Tangenten statt der Bogen gesetzt sind; sind ferner SM und SN die Perpendikel auf die Tangente: so ist Fläche SPp = ½Pp · SM, Fläche SQq = ½Qq · SN, also SPp : SQq = Pp · SM : Qq · SN. Nach §. 13. sind aber SPp und SQq den Zeiten proportional, und im vorliegenden Falle einander gleich und mit der Zeiteinheit identisch. Daher Pp · SM = Qq · SN oder Pp : Qq = SN : SM. Nach der Construction ist Pp : Qq = QB : AP = DQ' : DP' (Fig. 17).
   

   Fig. 226.

   Angenommen nun, die Linie TS träfe DP' nicht in D, sondern in einem am x davon entfernten Punkte F; so denke man sich ein Perpendikel FG auf TN gefällt. Es würde dann leicht folgen SM : DP' + x = SN : FG und da oben SM : DF = SN : DQ' jetzt DP' + x : DP' = FG : DQ'. Dies ist aber nicht möglich, weil DP' + x > DP' und FG < DQ; es muss daher TS durch D gehen.
7. No. 10. S. 62. Die Centripetalkraft verhält sich daher (nach §. 21.) direct wie $\scriptstyle {\frac {QR}{SP^{2}\cdot \ QT^{2}}}$ und indirect wie der Körper $\scriptstyle {\frac {SP^{2}\cdot \ QT^{2}}{QR}}$.
8. 

   Fig. 227.

   No. 11. S. 63. Eigentlich hat man, wenn PR eine Tangente in P ist, VP : PR = PQ : PR und daher $\scriptstyle VP={\frac {PR\ \cdot \ PQ}{QR}}$. Ist aber der Bogen PQ verschwindend klein, so wird QR ∥ VP, PR = PQ = $\scriptstyle \frown$ PQ und so $\scriptstyle VP={\frac {PQ^{2}}{QR}}$.
9. No. 12. S. 67. Sind in der Ellipse oder Hyperbel a' und b' conjugirte Halbmesser, α der Coordinatenwinkel, a und b die halben Hauptaxen, so ist bekanntlich a'b' sin α = ab.
10. No. 13. S. 67. Setzt man Pv = x', Qv = y', DC = b', CP = a', so stimmt die Proportion Pv · vG : Qv² = PC² : CD² (Fig. 23.) mit der bekannten Gleichung der Ellipse $\scriptstyle y'^{2}={\frac {b'^{2}}{a'^{2}}}\left(2a'x'-x'^{2}\right)$ überein.
11. No. 14. S. 68. Es wird nämlich Qv² + uP · Pv = Pv (uV + uP) = vP · P · V. Ferner ist uP = PT + Tv; vP = PT – Tv also uP · vP = PT² – Tv² und Qv² + uP · Pv = Qv² – Tv² + PT² = QT² + PT² = PQ².
12. No. 15. S. 68. Wenn Q mit P zusammenfällt, wird PF mit dem Perpendikel von C auf die Tangente identisch.
13. 

    Fig. 228.

    No. 16. S. 69. Die gemeinschaftliche halbe grosse Axe sei = a, die halbe kleine Axe CM = B, Cm = b, die Umlaufszeiten resp. T und t. Da die beschriebenen Flächenräume den Zeiten proportional sind, haben wir
    1.     T : t = aBπ : abπ = B : b

    Sind nun ACD, ACE gleichzeitig beschriebene Sectoren, so wird die Umlaufszeit desto kleiner, je grösser ein solcher Sector ist; also

    2.     T : t = ACD : ACE.

    Sind diese Sectoren aber sehr klein, so verhalten sie sich wie die Geschwindigkeiten im Punkt A oder nach §. 7.

    3.     ACE : ACD = EG : DG.

    Setzt man nun, der Kürze wegen, AG = x, so hat man $\scriptstyle DG^{2}={\frac {b^{2}}{a^{2}}}\left(2ax-x^{2}\right)EG^{2}={\frac {B^{2}}{a^{2}}}\left(2ax-x^{2}\right)$, also

    4.     DG : EG = b : B

    oder nach 2., 3. und 4. T : t = b : B, und nach 1. T : t = B: b, also

    5.     T : t = 1 : 1.

← Buch I. Abschnitt I.

Nach oben

Buch I. Abschnitt III. →

{{{ANMERKUNG}}}

Fertig! Dieser Text wurde zweimal anhand der Quelle Korrektur gelesen. Die Schreibweise folgt dem Originaltext.