in Bezug auf den Horizont, an welchem die Parallaxen bekanntlich ihre volle Grösse erhalten, dieselben vollständiger zu messen, und doch fanden wir, dass die Parallaxen um nicht mehr, als um eine Minute verschieden sind.
Neben der Entfernung des Mondes von der Erde sind auch die scheinbaren Durchmesser des Mondes und des Schattens veränderlich, weshalb wir auch von diesen reden müssen. Obgleich die Durchmesser der Sonne und des Mondes mittelst des Diopters des Hipparch richtig gemessen werden, so glaubt man doch, dies beim Monde viel genauer erreichen zu können mit Hülfe einiger auserwählter Mondfinsternisse, bei denen der Mond um gleich viel von seiner grössten und kleinsten Abside absteht; zumal wenn alsdann die Sonne in gleicher Weise sich dem so anschliesst, dass der Schattenkreis, welchen der Mond bei jeder derselben zu durchlaufen hat, gleich befunden wird; nur dass die Finsternisse sich auf ungleiche Theile erstrecken. Es ist nämlich offenbar, dass der Unterschied zwischen den verfinsterten Theilen und den entsprechenden Breiten des Mondes auf die Grösse des Bogens eines um den Mittelpunkt der Erde beschriebenen Kreises schliessen lässt, welchen der Durchmesser des Mondes einnimmt; — kennt man aber diesen, so findet man auch bald den Halbmesser des Schattens. Dies mag an einem Beispiele deutlicher gemacht werden. Wenn also zur Zeit der Mitte einer früheren Finsterniss drei Zoll vom Halbmesser des Mondes verfinstert sind, während seine Breite 47′ 54″ beträgt, und bei einer späteren, bei welcher die Breite 29′ 37″ war, zehn Zoll verfinstert wurden, so ist der Unterschied zwischen den Grössen der Finsternisse sieben Zoll, und derjenige zwischen den Breiten 18′ 17″, während 31′ 20″, als der scheinbare Durchmesser des Mondes, zwölf Zollen entsprechen. Es ergiebt sich also, dass der Mittelpunkt des Mondes zur Zeit der Mitte der ersten Finsterniss um den vierten Theil des Durchmessers desselben aus dem Schatten hervorragte, diesem entsprechen 7′ 50″ der Breite; und zieht man diese von den 47′ 54″ der ganzen Breite ab, so bleiben 40′ 4″ für den Halbmesser des Schattens. Ebenso reichte bei der zweiten Finsterniss der Schatten um den dritten Theil des Monddurchmessers, also um eine Breite von 10′ 27″, über den Mittelpunkt des Mondes hinaus; addirt man diese zu den 29′ 37″, so erhält man ebenfalls 40′ 4″ für den Halbmesser des Schattens[2]. Freilich ist des Ptolemäus’ Meinung, dass, während Sonne und Mond bei ihrer Conjunction und Opposition in ihren grössten Entfernungen von der Erde stehen, der Durchmesser des Mondes 31′ 20″ beträgt, und ebenso gross, behauptet er, den Durchmesser der Sonne durch das Diopter des Hipparch gefunden zu haben. Der Durchmesser des Schattens soll aber 1° 21′ 20″ sein,
Anmerkungen [des Übersetzers]
- ↑ [46] 323) Almagest V. 14.
- ↑ [46] 324)
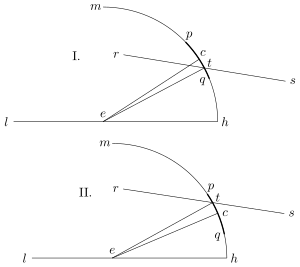
Die Figur I bezieht sich auf die erste der im Texte erwähnten Mondfinsternisse, die Figur II auf die zweite. In beiden Figuren liegen die Linien in der Ekliptik, und bezeichnen also die Axen des Schattens der Erde; die Bogen gehören den durch den Mittelpunkt des Mondes gelegten Längenkreisen an, der Theil derselben bezeichnet den Durchmesser des Mondes = 31′ 20″ = 12 Zoll; ist die in der Ebene des Längenkreises gelegene Grenzlinie des Erdschattens, welche den Monddurchmesser in trifft, während der Mittelpunkt des Mondes ist.
Nun ist der Winkel bei der ersten Finsterniss[WS 1] 47′ 54″, bei der zweiten 29′ 37″ und „ „ „ „ „ „ 7′ 50″, „ „ „ 10′ 27″ Differenz = 40′ 4″, Summa = 40′ 4″, wie im Text.
Anmerkungen (Wikisource)
- ↑ Vorlage: Finsternss
Nicolaus Copernicus: Nicolaus Coppernicus aus Thorn über die Kreisbewegungen der Weltkörper. Ernst Lambeck, Thorn 1879, Seite 231. Digitale Volltext-Ausgabe bei Wikisource, URL: https://de.wikisource.org/w/index.php?title=Seite:Kreisbewegungen-Coppernicus-0.djvu/259&oldid=- (Version vom 13.3.2017)










